Binary Search Tree - Read / Write

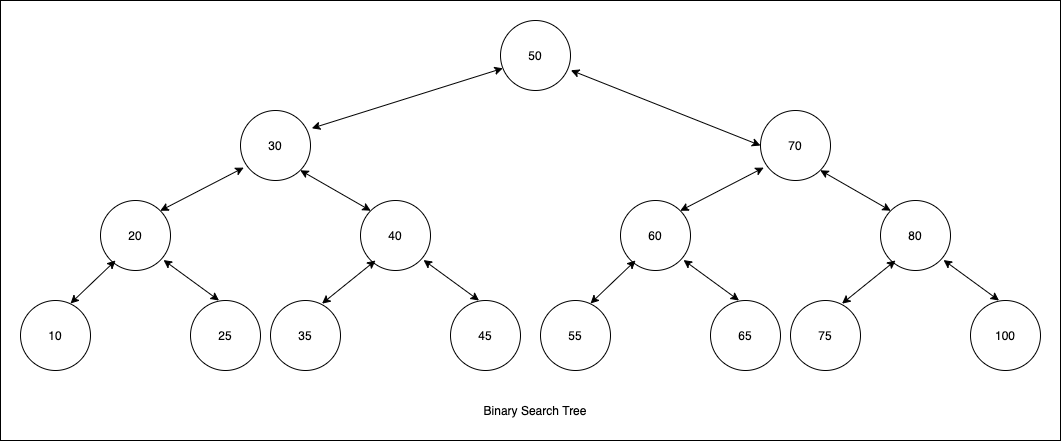
A binary search tree is a tree data structure that stores values in two sub-tree of left and right.

Properties

• If the node is the left child of its parent, then it must be smaller than (or equal to) the parent
• If the node is the right child of its parent, then it must be larger than the parent.
• All the nodes in the left subtree must be smaller (or equal) than the parent
• All the nodes in the right subtree must be larger than the parent

Tree node

This is the tree node that will store our tree structure data.

public class Tree {
    private int key;
    private Tree parent;
    private Tree left;
    private Tree right;

    // getters + setters
}

Generate

We can add a method to generate a tree from an array or a collection of items

public void generate(int[] array) {
    for (int i = 0; i < array.length; i++) {
        insert(array[i]);
    }
}

Insert

While inserting an entry to our tree, we need to find the position to fit. Entry will always be the leaf node considering the properties of a binary search tree. We have to search through the tree from the root to find an appropriate position of the newly inserted node.

• Check every node and compare the key
• If the key is less than the node, move left to the tree.
• If the key is greater than the node, move right to the tree

private void insert(int key) {
    Tree node = new Tree(key);
    if (root == null) {
        root = node;
        return;
    }
    Tree item = root;
    while (item != null) {
        if (key < item.getKey()) {
            if (item.getLeft() == null) {
                item.setLeft(node);
                node.setParent(item);
                break;
            }
            item = item.getLeft();
        } else {
            if (item.getRight() == null) {
                item.setRight(node);
                node.setParent(item);
                break;
            }
            item = item.getRight();
        }
    }
}

Find / Search

To find an entry in the tree, we have to search the tree recursively. If the key is less than the node then we have to move left otherwise, right.

private Tree findNode(Tree node, int key) {
    if (node == null)
        return null;
    if (node.getKey() == key) {
        return node;
    } else if (key < node.getKey()) {
        return findNode(node.getLeft(), key);
    } else {
        return findNode(node.getRight(), key);
    }
}

public boolean find(int key) {
    return findNode(root, key) != null;
}

Delete

While deleting a node from a tree, there can be three criteria to look

1. Node is a leaf, having no child nodes
2. Node has left / right child,
3. Node has both left and right children.

Leaf node

If the node is a leaf node, then we can set the parent node to null.

Having left / right child

If the node has a left / right child, then the parent will point to the child of the node.

Having both left and right child

If the node has both left and right children, then we have to follow these steps

1. Find successor of the node
2. Replace the node with the successor.
3. Successor will have the left and right child of the node.
4. Parent node will point to the successor.

Successor

To find the successor of the node, we need to follow these steps.

1. Move to the right child of the node.
2. Move to the way to the left most child. This child node will be the successor.

private Tree getSuccessor(Tree node) {
    var right = node.getRight();
    Tree successor = null;
    while (right != null) {
        successor = right;
        right = right.getLeft();
    }
    return successor;
}

The successor may contain the right child tree. In this case, the parent node of the successor will point to the right child and then replace the node with the successor.

public void delete(int key) {
    Tree node = findNode(root, key);
    if (node == null) {
        System.out.println("Key does not exist");
        return;
    }
    if (node.getLeft() == null && node.getRight() == null) {
        replaceNode(node, null);
    } else if (node.getLeft() == null) {
        replaceNode(node, node.getRight());
        node.setRight(null);
    } else if (node.getRight() == null) {
        replaceNode(node, node.getLeft());
        node.setLeft(null);
    } else {
        Tree successor = getSuccessor(node);
        replaceNode(successor, successor.getRight());

        successor.setLeft(node.getLeft());
        successor.setRight(node.getRight());
        replaceNode(node, successor);

        updateParent(successor.getLeft(), successor);
        updateParent(successor.getRight(), successor);

        node.setLeft(null);
        node.setRight(null);
    }
    node.setParent(null);
}

private void updateParent(Tree node, Tree parent) {
    if (node != null) {
        node.setParent(parent);
    }
}

private void replaceNode(Tree node, Tree replace) {
    if (node.getParent() == null) {
        root = replace;
        return;
    }
    if (node.getParent().getLeft() == node) {
        node.getParent().setLeft(replace);
    } else {
        node.getParent().setRight(replace);
    }
    updateParent(replace, node.getParent());
}

Height

Height of a binary search tree is the depth count from root to the leaf node.

public int height(Tree node) {
    if (node == null)
        return 0;
    return Math.max(height(node.getLeft()) + 1, height(node.getRight()) + 1);
}

Min

From the definition, the leftmost element will have the minimum item of the tree.

public int min(Tree node) {
    if (node == null)
        return Integer.MAX_VALUE;
    return Math.min(min(node.getLeft()), node.getKey());
}

Max

From the definition, the rightmost element will have the minimum item of the tree.

public int max(Tree node) {
    if (node == null)
        return Integer.MIN_VALUE;
    return Math.max(max(node.getRight()), node.getKey());
}

Complexity

In a balanced tree (best case), the complexity is O(log n).
In the worst case, if the data is sorted, then the tree will behave like a linked list with the complexity is O(n).

Operation	Best case	Worst case
Insert	O(log n)	O(n)
Search	O(log n)	O(n)
Delete	O(log n)	O(n)
Min	O(log n)	O(n)
Max	O(log n)	O(n)
Height	O(n)	O(n)